Deep Learning in Python: Computational Graphs

In deep learning frameworks like TensorFlow, Torch, and Theano, backpropagation is implemented using computational graphs. More importantly, understanding backpropagation through computational graphs combines several different algorithms and their variations, such as backpropagation through time and backpropagation with shared weights. Once everything is converted to a computational graph, it’s still the same algorithm—just backpropagation on a computational graph.

What is a Computational Graph

A computational graph is defined as a directed graph where nodes correspond to mathematical operations. A computational graph is a way to express and evaluate mathematical expressions.

For example, here’s a simple mathematical equation:

p = x + y

We can draw the computational graph for the above equation as shown below.

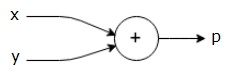
The above computational graph has an addition node (the one with the “+” sign), two input variables x and y, and one output q.

Let’s take another, slightly more complex example. We have the following equation.

g = left (x+y right ) ast z

The above equation is represented by the following computational graph.

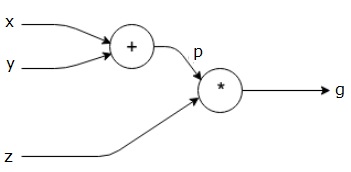
Computation Graph and Backpropagation

Computation graphs and backpropagation are both important core concepts for training neural networks in deep learning.

Forward Pass

A forward pass is the procedure for evaluating the value of a mathematical expression represented by a computation graph. Performing a forward pass means forwarding the values of variables from the left (inputs) to the right (outputs).

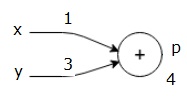
Let’s consider an example where all inputs are assigned values. Suppose all inputs have the following values.

x=1, y=3, z=-3

Given these input values, we can perform a forward pass and get the following output values at each node.

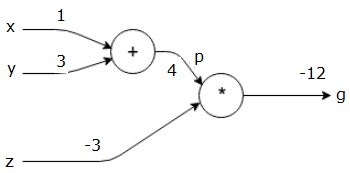
First, we use the values of x=1 and y=3 to get p=4.

Then we use p=4 and z=-3 to get g=-12. We proceed from left to right, moving forward.

Goal of the Backward Pass

In the backward pass, our goal is to compute the gradient of each input with respect to the final output. These gradients are crucial for training neural networks using gradient descent.

For example, we would like to have the following gradients.

Desired Gradient

frac{partial x}{partial f}, frac{partial y}{partial f}, frac{partial z}{partial f}

Backward Propagation

We begin the backward propagation by finding the derivative of the final output with respect to the final output (itself!). Therefore, it will result in the identity derivative, which is equal to 1.

frac{partial g}{partial g} = 1

Our computation graph now looks like this –

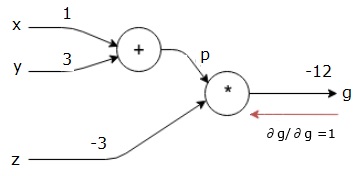
Next, we will perform a backward pass using the ““ operation. We will calculate the gradients of p and z. Since g = p

Steps to Train a Neural Network

Follow these steps to train a neural network –

• For a data point x in the dataset, we perform a forward pass with x as input and calculate the cost c as output.

• We perform a backward pass starting at c and compute the gradients for all nodes in the graph. This includes the nodes representing the neural network weights.

• We then update the weights by W = W – learning rate * gradient.

• We repeat this process until we reach the stopping criterion.