Python Data Structures: Divide and Conquer

In the divide and conquer approach, the problem at hand is divided into smaller subproblems, each of which is then solved independently. As we continue to divide the subproblems into smaller ones, we may eventually reach a stage where further division becomes impossible. The smallest possible subproblems (fractions) are then solved, each “atomic” in their own right. The solutions to all subproblems are eventually combined to obtain a single solution to the original problem.

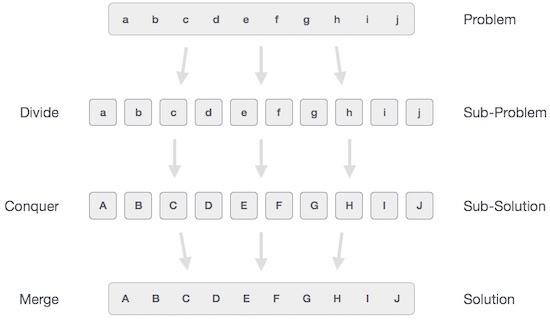
In general, the divide and conquer approach can be understood in three steps.

Split/Break

This step involves breaking the problem into smaller subproblems. Each subproblem should represent a portion of the original problem. This step typically involves recursively dividing the problem until no further subproblems can be divided. At this stage, the subproblems become atomic in nature, but still represent a portion of the actual problem.

Conquer/Solve

This step presents a number of smaller subproblems to be solved. Generally, at this level, the problem is considered to have “solved” itself.

Merge/Comb

Once the smaller subproblems are solved, this stage recursively combines them until a solution to the original problem is formed. This algorithmic approach works recursively, with the conquer and merge steps working so closely that they appear to be one.

Example

The following program is an example of the divide and conquer programming approach, using binary search implemented in Python.

Binary Search Implementation

In a binary search, we take a sorted list of elements and begin searching for an element in the middle of the list. If the search value matches the middle value in the list, we complete the search. Otherwise, we choose to search from the right or left half of the list, depending on the value of the searched item, thereby removing half of the elements from the list.

This is possible because the list is sorted, making it much faster than a linear search. Here, we divide the given list and conquer by selecting the appropriate half. We repeat this method until we find the element or conclude that it does not exist in the list.

Example

def bsearch(list, val):
   list_size = len(list) - 1
   idx0 = 0
   idxn = list_size
# Find the middle most value
   while idx0 <= idxn:
      midval = (idx0 + idxn)// 2
      if list[midval] == val:
         return midval
# Compare the value the middle most value
   if val > list[midval]:
      idx0 = midval + 1
   else:
      idxn=midval-1
   if idx0 > idxn:
      return None
#Initialize the sorted list
list = [2,7,19,34,53,72]

# Print the search result
print(bsearch(list,72))
print(bsearch(list,11))

Output

When the above code is executed, it produces the following result –

5
None