Deep Learning with Python: Deep Neural Networks

A deep neural network (DNN) is a type of neural network with multiple hidden layers between the input and output layers. Similar to shallow ANNs, DNNs can model complex nonlinear relationships.

The main purpose of a neural network is to take a set of inputs, perform progressively complex computations on them, and produce an output to solve real-world problems, such as classification. We will limit ourselves to feedforward neural networks.

In a deep network, we have one input, one output, and a sequential data stream.

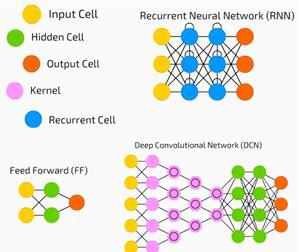
Neural networks are widely used in supervised learning and reinforcement learning problems. These networks are based on a set of interconnected layers.

In deep learning, the number of hidden layers, most of which are nonlinear, can be very large; for example, around 1,000 layers.

DL models produce much better results than regular ML networks.

We mostly use gradient descent to optimize the network and minimize the loss function.

We can use Imagenet, a database of millions of digital images, to classify the dataset into categories such as cats and dogs. In addition to static images, DL networks are increasingly being used for dynamic images, as well as time series and text analysis.

Training datasets form an important part of deep learning models. Furthermore, backpropagation is the primary algorithm for training DL models.

DL deals with training large neural networks with complex input-output transformations.

An example of DL is mapping photos to the names of the people in the photos, as is done on social networks. Describing a photo with a phrase is another recent application of DL.

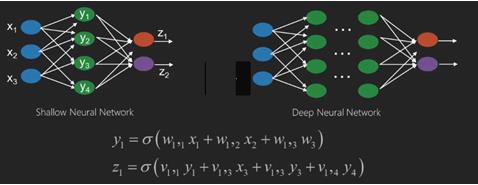
A neural network is a function whose inputs, such as x1, x2, x3, etc., are transformed into outputs, such as z1, z2, z3, and so on, via two (shallow networks) or a few intermediate operations (deep networks).

The weights and biases of each layer change. ‘w’ and ‘v’ are the weights or synapses of each layer of the neural network.

The best use case for deep learning is supervised learning problems. Here, we have a large amount of data input and a set of desired outputs.

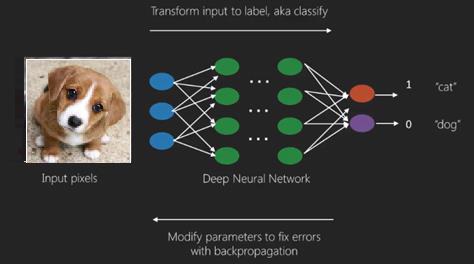
Here, we apply the backpropagation algorithm to obtain the correct output prediction.

The most fundamental dataset for deep learning is MNIST, a dataset of handwritten digits.

We can use Keras to train a deep convolutional neural network to classify images of handwritten digits from this dataset.

The emission, or activation, of a neural network classifier produces a score. For example, to classify a patient as sick or healthy, we consider parameters such as height, weight, temperature, and blood pressure.

A high score means the patient is sick, while a low score means they are healthy.

Each node in the output layer and hidden layer has its own classifier. The input layer accepts the input and passes its score to the next hidden layer for further activation, and so on until the output.

This forward progression from input to output, from left to right, is called forward propagation.

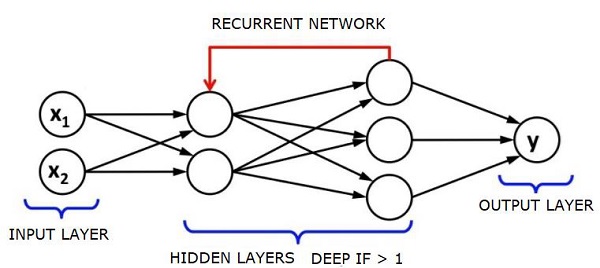
A credit assignment path (CAP) in a neural network refers to a series of transformations from input to output. CAP describes the possible causal relationships between input and output.

The CAP depth, or CAP depth, of a given feedforward neural network is the number of hidden layers plus one, since the output layer is also included. For recurrent neural networks, where a signal can propagate through a layer several times, the CAP depth can be infinite.

Deep and Shallow Networks

There is no clear depth threshold that demarcates shallow learning from deep learning; however, it is generally accepted that for deep learning with multiple nonlinear layers, the CAP must be greater than 2.

The basic node of a neural network is a perceptron, modeled after the neurons in biological neural networks. Then there are multilayer perceptrons, or MLPs. Each set of inputs is modified by a set of weights and biases; each edge has a unique weight, and each node has a unique bias.

The accuracy of a neural network’s predictions depends on its weights and biases.

The process of improving a neural network’s accuracy is called training. The output of the forward prediction network is compared to known correct values.

The cost function, or loss function, is the difference between the generated output and the actual output.

The focus of training is to minimize the training cost over millions of training examples. To achieve this, the network adjusts the weights and biases until the predictions match the correct outputs.

Once well-trained, a neural network is likely to make accurate predictions every time.

When patterns become complex and you want your computer to be able to recognize them, you must choose a neural network. In the case of such complex patterns, neural networks outperform all other competing algorithms.

Now with GPUs, they can be trained much faster than before. Deep neural networks are already revolutionizing the field of artificial intelligence.

Computers have proven excellent at performing repetitive calculations and following detailed instructions, but not so good at recognizing complex patterns.

When faced with simple pattern recognition, support vector machines (SVMs) or logistic regression classifiers work well, but as the complexity of the patterns increases, deep neural networks become the only solution.

Thus, for complex patterns like faces, shallow neural networks fail, forcing the use of deep neural networks with many layers. Deep neural networks work by breaking down complex patterns into simpler ones. For example, in the case of a face, a deep network uses edges to detect parts like lips, nose, eyes, and ears, and then reassembles these parts to form a face.

The accuracy of correct predictions has become so high that a deep network recently defeated humans at the Google Pattern Recognition Challenge.

The idea of layered perceptron networks has been around for some time; in this area, deep nets mimic the human brain. One drawback is that they take a long time to train, a hardware constraint.

However, recent high-performance GPUs can now train such deep nets in a week; fast CPUs might take weeks or even months to do the same.

Choosing a Deep Net

How do we choose a deep net? We must decide whether we want to build a classifier or find patterns in the data, and whether we want to use unsupervised learning. To extract patterns from a set of unlabeled data, we use a restricted Boltzmann machine or an autoencoder.

Consider the following when choosing a deep net

• For text processing, sentiment analysis, parsing, and named entity recognition, we use recurrent nets or recursive neural tensor networks, or RNTNs.

• For any language model operating at the character level, we use recurrent nets.

• For image recognition, we use deep belief networks (DBNs) or convolutional networks.

• For object recognition, we use RNTNs (RNTs) or convolutional networks.

• For speech recognition, we use recurrent networks (RNNs).

In general, deep belief networks and multilayer perceptrons with rectified linear units (RELUs) are good choices for classification.

For time series analysis, we always recommend using recurrent networks.

Neural networks have been around for over 50 years; however, they have only recently risen to prominence. The reason is that they are difficult to train; when we try to train them using a method called backpropagation, we encounter a problem called vanishing or exploding gradients. When this happens, training takes longer and accuracy suffers. When training a dataset, we continuously calculate the cost function, which is the difference between the predicted output and the actual output for a set of labeled training data. The cost function is then minimized by adjusting the weights and bias values until the lowest value is achieved. The training process uses the gradient, which is the rate at which the cost changes with changes in the weight or bias values.

Restricted Boltzmann Networks or Autoencoders – RBNs

In 2006, a breakthrough was achieved in addressing the vanishing gradient problem. Geoff Hinton devised a new strategy that led to the development of the Restricted Boltzmann Machine (RBM), a shallow two-layer network.

The first layer is the visible layer, and the second layer is the hidden layer. Every node in the visible layer is connected to every node in the hidden layer. This network is called a restricted network because no two layers in the same layer are allowed to share a connection.

Autoencoders are networks that encode input data into vectors. They create a hidden, or compressed, representation of the original data. Vectors are useful in dimensionality reduction; they compress the original data into a smaller number of essential dimensions. An autoencoder paired with a decoder allows reconstruction based on the hidden representation of the input data.

An RBM is mathematically equivalent to a two-way translator. A forward pass takes the input and translates it into a set of numbers that encode the input. Simultaneously, a backward pass translates this set of numbers into the reconstructed input. A well-trained network can perform the inverse translation with high accuracy.

In both steps, the weights and biases play a key role; they help the RBM decode the relationships between the inputs and determine which inputs are important for detecting patterns. Through forward and backward passes, the RBM is trained to reconstruct the input using different weights and biases until the input closely matches its reconstruction. An interesting aspect of RBMs is that the data does not need to be labeled. This is crucial for real-world datasets such as photos, videos, sounds, and sensor data, all of which are often unlabeled. Instead of requiring humans to manually label the data, RBMs automatically classify it; by appropriately adjusting the weights and biases, the RBM is able to extract important features and reconstruct the input. RBMs are part of a family of feature extractor neural networks designed to identify inherent patterns in data. These are also called autoencoders because they must encode their own structure.

Deep Belief Networks – DBNs

Deep Belief Networks (DBNs) are formed by combining RBMs with a clever training method. We have a new model that finally solves the vanishing gradient problem. Geoff Hinton invented RBMs and also developed deep belief networks as an alternative to backpropagation.

DBNs are similar in structure to MLPs (Multi-Layer Perceptrons), but differ significantly in training. It’s the training that allows DBNs to outperform their shallow counterparts.

A DBN can be thought of as a stack of RBMs, where the hidden layers of one RBM are the visible layers of the RBM above it. The first RBM is trained to reconstruct its input as accurately as possible.

The hidden layers of the first RBM are used as the visible layers of the second RBM, which is trained using the output of the first RBM. This process repeats until every layer in the network has been trained.

In a DBN, each RBM learns the entire input. DBNs work globally by continuously fine-tuning the entire input, as the model slowly improves, just as a camera lens slowly focuses a photograph. A stack of RBMs outperforms a single RBM, just as a multilayer perceptron (MLP) outperforms a single perceptron.

At this stage, the RBMs have detected inherent patterns in the data, but without any names or labels. To complete DBN training, we must introduce labels for these patterns and fine-tune the network through supervised learning.

We need a very small set of labeled examples in order to associate features and patterns with a name. This small labeled dataset is used for training. This set of labeled data can be very small compared to the original dataset.

The weights and biases are slightly altered, resulting in small changes in the network’s perception of patterns and, typically, a small improvement in overall accuracy.

Training can also be completed in a reasonable amount of time using GPUs, and the results are very accurate compared to shallow nets, and we’ve also seen a solution to the vanishing gradient problem.

Generative Adversarial Networks – GANs

Generative adversarial networks are deep neural networks composed of two networks that are set against each other, hence the term “adversarial.”

GANs were introduced in a 2014 paper by researchers at the University of Montreal. Facebook AI expert Yann LeCun, referring to GANs, called adversarial training “the most interesting idea in ML in the past 10 years.”

The potential of GANs is enormous, as the networks learn to mimic the distribution of any data. GANs can be taught to create parallel worlds in any domain that are strikingly similar to our own: images, music, speech, prose. They are, in a sense, robotic artists, and their output is quite impressive.

In a GAN, one neural network, called the generator, generates new data instances, while another, called the discriminator, evaluates their authenticity.

Let’s say we’re trying to generate handwritten digits like those in the MNIST dataset, which comes from the real world. The discriminator’s job is to identify them as real when presented with examples from the real MNIST dataset.

Now consider the following steps of a GAN.

• The generator network takes input in the form of random numbers and returns an image.

• This generated image is fed as input to the discriminator network, along with a stream of images from the real dataset.

• The discriminator takes real and fake images and returns a probability, a number between 0 and 1, with 1 representing a realistic prediction and 0 representing a fake.

• This creates a double feedback loop −

  • The discriminator feeds back into the ground truth about the image.

  • The generator and the discriminator are in a feedback loop.

Recurrent Neural Networks – RNNs

RNNs are neural networks in which data can flow in either direction. These networks are used in applications such as language modeling and natural language processing (NLP).

The basic concept of RNNs is to exploit sequential information. In a normal neural network, all inputs and outputs are assumed to be independent of each other. If we want to predict the next word in a sentence, we must know the previous words.

RNNs are called recurrent because they repeat the same task for each element in the sequence, and the output is based on previous computations. Therefore, RNNs can be said to have a “memory” that captures information about previous computations. In theory, RNNs can use information from very long sequences, but in reality, they can only look back a few steps.

Long Short-Term Memory (LSTM) networks are the most commonly used RNNs.

Along with convolutional neural networks, RNNs have been used as part of models to generate descriptions for unlabeled images. This seems to be quite impressive.

Convolutional Deep Neural Networks – CNNs

Increasing the number of layers in a neural network, making it deeper, increases its complexity and allows us to model more complex functions. However, the number of weights and biases increases exponentially. In fact, learning such difficult problems may become impossible for normal neural networks. This led to a solution: convolutional neural networks.

CNNs are widely used in computer vision and are also applied to acoustic modeling for automatic speech recognition.

The idea behind convolutional neural networks is to pass a “moving filter” through an image. This moving filter, or convolution, is applied to a certain neighborhood of a node—perhaps a pixel, for example—where the applied filter is 0.5x the node’s value.

Famous researcher Yann LeCun pioneered convolutional neural networks. Facebook uses these networks for its facial recognition software. CNNs have long been the go-to solution for machine vision projects. Convolutional networks have many layers. In the 2015 Imagenet Challenge, a machine was able to beat humans at object recognition.

In short, a convolutional neural network (CNN) is a multi-layered neural network. These layers can sometimes number as many as 17 or more, and the input data is assumed to be images.

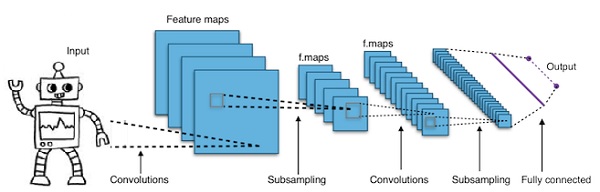
CNNs significantly reduce the number of parameters that need to be tuned. Therefore, CNNs effectively handle the high dimensionality of the original image.