Python Design Patterns: Collections

A collection can be defined as an unordered collection that is iterable, mutable, and contains no duplicate elements. In Python, the Set class is a notation for a mathematical set. The main advantage of using a collection is that it includes highly optimized methods for inspecting specific elements.

Python includes a separate category called frozensets. These collections are immutable objects that support only methods and operators that produce the desired results.

How to Implement Sets

The following program helps implement sets:

# Set in Python

# Creating two sets
set1 = set()
set2 = set()

# Adding elements to set1
for i in range(1, 6):
set1.add(i)

# Adding elements to set2
for i in range(3, 8):
set2.add(i)

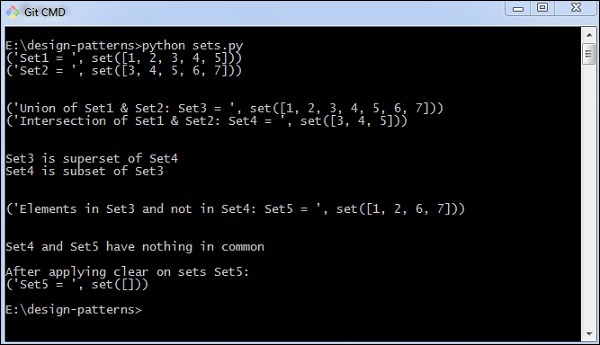
print("Set1 = ", set1)
print("Set2 = ", set2)
print("n")

# Union of set1 and set2
set3 = set1 | set2# set1.union(set2)
print("Union of Set1 & Set2: Set3 = ", set3)

# Intersection of set1 and set2
set4 = set1 & set2# set1.intersection(set2)
print("Intersection of Set1 & Set2: Set4 = ", set4)
print("n")

# Checking relation between set3 and set4
if set3 > set4: # set3.issuperset(set4)
   print("Set3 is superset of Set4")
elif set3 < set4: # set3.issubset(set4)
   print("Set3 is subset of Set4")
else : # set3 == set4
   print("Set3 is same as Set4")

# displaying relation between set4 and set3
if set4 < set3: # set4.issubset(set3)
   print("Set4 is subset of Set3") print("n")

# Difference between set3 and set4
set5 = set3 - set4
print("Elements in Set3 and not in Set4: Set5 = ", set5)
print("n")

# Check if set4 and set5 are disjoint sets
if set4.isdisjoint(set5):
print("Set4 and Set5 have nothing in common")

# Removing all the values of set5
set5.clear()

print("After applying clear on sets Set5: ")
print("Set5 = ", set5)

Output

The above program produces the following output –

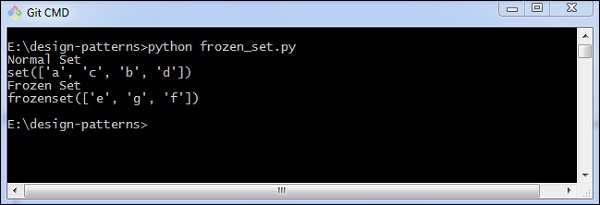
The following program can be used to demonstrate frozen sets of data:

normal_set = set(["a", "b", "c"])

# Adding an element to a normal set is fine
normal_set.add("d")

print("Normal Set")
print(normal_set)

# A frozen set
frozen_set = frozenset(["e", "f", "g"])

print("Frozen Set")
print(frozen_set)

Output

The above program produces the following output –