Python Functors and Applicative Functors

Python Functors and Applicative Functors. Functors are functional representations of simple data. The functor version of the number 3.14 is a zero-argument function that returns that value. Here’s an example:

>>> pi = lambda: 3.14
>>> pi()
3.14

This creates an anonymous function object with zero arguments and returns a simple value.

When you apply a curried function to a functor, you create a new curried functor. The concept can be summarized as follows: by using functions to represent arguments, values, and the function itself, you can apply functions to arguments to get values.

Once everything in a program is a function, all computation is simply a variation of the functional composition model. Both the arguments and the results of a curried function can be functors. Sometimes you can use the getValue() method on a functor object to get a simple Python-compatible type that can be used in non-curried code.

Because programming is based on functional composition, no computation is required before actually requesting a value using the getValue() method. Instead of performing a lot of intermediate computation, the program defines complex intermediate objects to generate the requested value. In principle, a smarter compiler or runtime system could optimize this composition.

When applying functions to functor objects, we use a method similar to map(), which is equivalent to the * operator. You can understand the role of functors in expressions by using the function * functor or map(function, functor) methods.
To properly handle functions with multiple arguments, you can construct compound functors using the & operator. The functor & functor method is often used to construct a functor object from a pair of functors.

You can use subclasses of the Maybe functor to encapsulate Python’s simple types. The interesting thing about the Maybe functor is that it can be used to properly handle missing data. Chapter 11 used this approach by decorating built-in functions to be aware of the None value. The PyMonad library uses this approach by decorating data to exclude it.
The functor Maybe has two subclasses:

• Nothing
• Just(some simple value)

Nothing is used instead of the Python simple value None to represent missing data. Just(some simple value) is used to wrap all other Python objects. These functors are function-like representations of constant values.

You can use curried functions on these Maybe objects to properly handle missing data, as shown below:

>>> x1 = systolic_bp * Just(25) & Just(50) & Just(1) & Just(0)
>>> x1.getValue()
116.09

>>> x2 = systolic_bp * Just(25) & Just(50) & Just(1) & Nothing
>>> x2.getValue() is None
True

The operator * composes the systolic_bp() function with the argument composition. The operator & constructs a composite functor that can be passed as an argument to a curried function with multiple arguments.

This indicates that a value is returned, not a TypeError exception. This is particularly useful when dealing with large, complex datasets that may contain missing or invalid data, and is much better than decorating all functions to be aware of the None value.

This approach is particularly useful for curried functions. Because the functor has very few methods, the Maybe functor cannot be used in non-curried Python code.

In non-curried Python code, you must use the getValue() method to retrieve simple Python values.

Using the Lazy List() Functor

People new to the List() functor may find it confusing because, unlike Python’s built-in list type, it is very “lazy.” When the built-in list(range(10)) method is evaluated, the list() function evaluates the range() object to create a list of 10 items. However, PyMonad’s List() functor is so lazy that it doesn’t even do this computation.

Compare the two below:

>>> list(range(10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> List(range(10))
[range(0, 10)]

The List() functor does not evaluate the range() object; it simply holds onto it without evaluating it. The pymonad.List() function is useful for collecting functions without evaluating them.

The use of range() can be confusing. The range() object in Python 3 is also lazy, so the example includes two levels of deferred execution. pymonad.List() creates items on demand. Each item in List is a range() object that can be evaluated to produce a sequence of values.

The List functor can be evaluated later as needed:

>>> x = List(range(10))
>>> x
[range(0, 10)]
>>> list(x[0])
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

This creates a lazy List object containing a range() object. The range() object at position 0 in the list is then extracted and evaluated.

The List object does not evaluate the generator function or the range() object; it treats any iterable argument as a single iterable object. However, we can use the * operator to extend the value of a generator or range() object.

Note that the * operator has several meanings: it’s the built-in mathematical multiplication operator, the functional composition operator defined by PyMonad, and a built-in modifier that binds a single sequence object to all positional arguments when a function is called. Below, we’ll use its third meaning to assign a sequence to multiple positional arguments.

The curried version of the range() function is shown below, with a lower bound of 1 instead of 0. This can be convenient for some mathematical operations because it avoids the complexity of positional arguments in the built-in range() function.

@curry
def range1n(n):
if n == 0: return range(1, 2) # Only the value 1
return range(1, n+1)

This simply wraps the built-in range() function and curries it using the PyMonad package.

Since a List object is a functor, we can map a function onto it.

Apply a function to each item in a List object. The following example shows:

>>> fact= prod * range1n
>>> seq1 = List(*range(20))
>>> f1 = fact * seq1
>>> f1[:10]
[1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880]

This defines a composite function, fact(), which is constructed from the previous prod() and range1n() functions and is a factorial function. It also creates a List() functor, seq1, which is a sequence of 20 values. It also maps the fact() function to the seq1 functor, creating a sequence of factorial values, f1. It also checks the first 10 values.

Composition of multiple functions has some similarities to composition of functions and functors. Both prod*range1n and fact*seq1 use functional composition. Obviously, the former composes functions, while the latter composes functions and functors.

Another small function to extend this example is as follows:

@curry
def n21(n):
return 2*n+1

This small function, n21(), performs a small calculation. However, because it is curried, it can be applied to a functor, such as the List() function. The second part of the above example is as follows:

>>> semi_fact = prod * alt_range
>>> f2 = semi_fact * n21 * seq1
>>> f2[:10]
[1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425, 654729075]

This defines a composite function using the previous prod() and alt_range() functions. Function f2 is a semi-factorial (double factorial) function. By mapping the small function n21() to the seq1 sequence to construct the values of the function f2, a new sequence is created. The semi_fact function is then applied to this new sequence to create a set of sequence values corresponding to the values in the original sequence.
Next, the / operator can be mapped to the map() and operator.truediv operators in parallel.

>>> 2*sum(map(operator.truediv, f1, f2))
3.1415919276751456

The map() function applies the given operator to two operators and generates a sequence to which fractions can be added.

The f1 & f2 method creates all possible combinations of values from two List objects. This is one of the key features of List objects—it’s easy to enumerate all possible combinations, allowing simple algorithms to compute and filter out all possible subsets. However, this isn’t what we want, which is why we use the map() function instead of the operator.truediv * f1 & f2 method.

We’ve defined a fairly complex computation using some functional composition techniques and a functor class definition. The full definition of this computation is as follows:

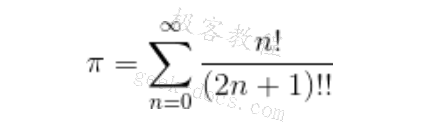
Ideally, rather than using a fixed-size List object, we would like to have a lazily evaluated, potentially infinite sequence of integer values. We could then use the sum() function and a curried version of the takewhile() function to sum the values until they become too small to meaningfully affect the result. This requires a lazier version of the List() object to work with the itertools.counter() function. PyMonad 1.3 doesn’t have such a potentially infinite list, so we have to use the fixed-size List() object.