SciPy ODR

ODR stands for Orthogonal Distance Regression and is used in regression research. Basic linear regression is often used to estimate the relationship between two variables, y and x, by drawing a line of best fit on a graph.

The mathematical method used for this is called the method of least squares, and its goal is to minimize the sum of the squared errors at each point. The key question here is how do you calculate the error (also called the residual) at each point?

In standard linear regression, the goal is to predict the Y value from the X value—so it’s sensible to calculate the error in the Y value (shown as the gray line in the figure below). However, sometimes it’s more sensible to consider the errors in both X and Y (shown as the red dashed line in the figure below).

For example—when you know your measurement of X is uncertain, or when you don’t want to focus on the error in one variable over the other.

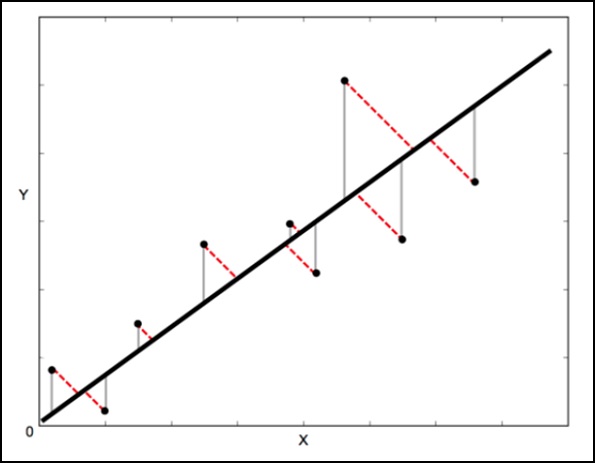
Orthogonal distance regression (ODR) is one method that can do this (orthogonal here means perpendicular – so it calculates the error perpendicular to the line, not just “perpendicular”).

Scipy.odr Implementation of Univariate Regression

The following example demonstrates the implementation of univariate regression using scipy.odr.

import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random

# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])

# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
   m, c = p
   return m*x + c

# Create a model for fitting.
linear_model = Model(linear_func)

#Create a RealData object using our initiated data from above.
data = RealData(x, y)

# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])

# Run the regression.
out = odr.run()

# Use the in-built pprint method to give us results.
out.pprint()

The above program will produce the following output.

Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [0.7786442 2.33126407]

Beta Covariance: [
   [1.93150969-4.82877433]
   [-4.82877433 17.31417201
]]

Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
   Sum of squares convergence