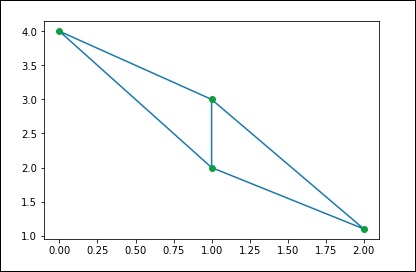
Delaunay Triangulation Computation

Let’s understand what Delaunay triangulations are and how they are used in SciPy.

What are Delaunay Triangulations

In mathematics and computational geometry, for a set of discrete points P on a plane, a Delaunay triangulation is a triangulation DT(P) such that no point in P lies within the circumference of any triangle in DT(P).

We can compute the same result using SciPy. Let’s consider the following example.

from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()

The above program will produce the following output.

Coplanar Points

Let’s understand what coplanar points are and how they are used in SciPy.

What are Coplanar Points

Coplanar points are three or more points that lie in the same plane. Recall that a plane is a flat surface that extends endlessly in all directions. In math textbooks, it is often shown as a quadrilateral.

Let’s see how to find this point using SciPy. Let’s consider the following example.

from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanar

The above program will produce the following output.

array([[4, 0, 3]], dtype = int32)

This means that point 4 is near triangle 0 and vertex 3, but is not included in the triangle.

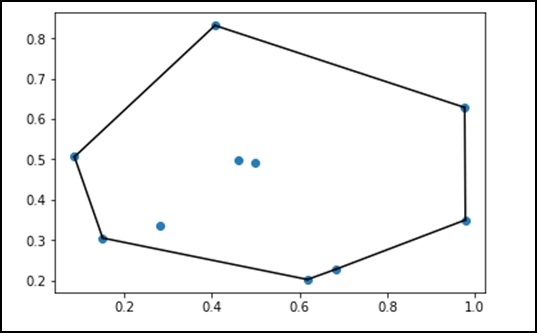
Convex Polyhedrons

Let’s understand what convex polyhedrons are and how they are used in SciPy.

What is a Convex Polyhedron?

In mathematics, the convex hull or convex envelope of a set of points X in the Euclidean plane or Euclidean space (or more generally, in affine space over the real numbers) is the smallest convex set that contains X.

Let’s consider the following example to understand this in more detail.

from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()

The above program will produce the following output.